Le sudoku est une sorte de puzzle qui se joue sur une grille de neuf cases par neuf cases contenant chacune un chiffre entre 1 et 9. Chaque ligne, chaque colonne et chacun des neuf carrés de trois par trois doit contenir chacun de ces neuf chiffres une et une seule fois.
Les ordinateurs sont supérieurs aux humains pour ce qui est de la capacité à faire des calculs. Les humains sont supérieurs en termes d'intuition, d'ingéniosité et de réflexion. Chacun doit donc utiliser ses points forts.
La méthode de résolution la plus simple avec un ordinateur est de tester toutes les possibilités jusqu'à trouver la bonne. Dans la première case vide on met un 1 et on vérifie que le résultat est valide. Si c'est le cas on passe à la case suivante et on met un 1, etc. Si la grille n'est pas valide, on essaie avec un 2, puis un 3, etc.
La figure ci-contre montre que l'algorithme essaie un 1 dans la première case libre puis un 1 dans la deuxième, ce qui est évidemment impossible donc il passe immédiatement à un 2, etc. (les données initiales sont en rouge et les chiffres essayés par le programme en bleu).
Si le 1 dans la première case ne pose pas de problème mais qu'aucun chiffre n'est valide dans la deuxième case libre ça signifie que le 1 n'est pas en fait possible. Donc on l'enlève et on met un 2 à la place. La figure montre bien que l'algorithme revient parfois ainsi sur ses pas.
Cette méthode essaie toutes les possibilités l'une après l'autre. Si une solution existe elle finira donc bien par la trouver — même si la grille de sudoku est dite « difficile » ou niveau « expert » ou « diabolique ». En revanche elle tente même des solutions ineptes (la première combinaison essayée aura deux 1 sur la première ligne).
Cette méthode ne traite pas différemment les grilles que les joueurs considèrent facile et difficile, et ne permet donc pas d'évaluer le niveau de difficulté d'une grille.
Si l'ordinateur essaie les chiffres dans l'ordre croissant, une grille dont la première case vide doit avoir un 9 prendra beaucoup de temps. Cette méthode ne respecte donc pas ce qu'on appelle les invariants : permuter tous les 1 et tous les 9 ne change pas vraiment la grille, donc la méthode de résolution ne devrait pas avoir plus de mal avec une variante qu'avec l'autre. Pour un mathématicien, n'avoir aucun mal avec un certain problème mais beaucoup plus avec un autre complètement équivalent est très louche.
Une variante utilise une méthode stochastique, qui par définition fait intervenir le hasard. D'abord, on choisit une valeur au hasard pour chaque case vide. Ensuite, on modifie les chiffres au hasard de manière répétée pour réduire le nombre d'incohérences (comme deux fois le même chiffre sur une ligne), par exemple avec un recuit simulé, un algorithme génétique ou un mélange des deux.
C'est plus rapide (mais plus compliqué à programmer) que la force brute. En revanche, c'est tout aussi frustrant pour un humain parce qu'il ne semble pas y avoir de logique à la méthode et parce que l'algorithme livre une solution sans fournir d'étapes intermédiaires.
Les grilles de sudoku ont été créées pour des joueurs humains, donc les premières tactiques inventées l'ont été par des humains avec un mode de pensée humain. C'est-à-dire en faisant preuve de logique et en se basant sur des déductions.
La tactique la plus simple est de trouver une ligne, une colonne ou un carré ayant déjà huit chiffres. Dans ce cas la valeur du neuvième est évidente.
Malheureusement, ça n'arrive pas si souvent. La tactique suivante est de procéder par élimination : quelles valeurs sont impossibles pour une certaine case : il y a déjà un 1 sur cette ligne et un 2 dans cette colonne, etc. En procédant ainsi par élimination, on peut tenir, pour chaque case, une liste des valeurs possibles.
Si on veut formaliser cette procédure (par exemple pour l'implémenter dans un programme informatique), on commence par dire qu'a priori la case peut contenir n'importe lequel des neuf chiffres. Ensuite, on passe toutes les cases en revue (avec une boucle for) et pour chaque case on regarde toutes les cases sur sa ligne, dans sa colonne et dans son carré (nouvelles boucles for). Quand on passe en revue chacune des huit cases de sa ligne par exemple, on va dire « cette case contient un 4 donc notre case ne peut pas avoir de 4 » et on raye 4 de la liste des possibilités.
Une fois qu'on a fait ça avec toutes les cases libres, on va trouver que certaines cases n'ont qu'une seule valeur possible (mettons 6). Dans ce cas, on recommence (on itère) en tenant compte de cette information on raye 6 de la liste des possibilités pour toutes les cases sur sa ligne, dans sa colonne et dans son carré.
Cette méthode suffit pour trouver la solution des grilles les plus simples. Pour les cas plus compliqués, il faut être un peu plus rusé.
On peut chercher des paires. Si deux cases de la même ligne, colonne ou carré ont pour seules valeurs possibles 5 et 7 alors on sait que l'une des deux vaudra 5 et l'autre 7 (même si on ne sait pas laquelle vaut quoi). On peut donc éliminer 5 et 7 pour les sept autres cases. Informatiquement ça veut dire passer en revue toutes les lignes, toutes les colonnes et tous les carrés (encore des boucles for) et pour chacune comparer toutes les paires de cases (double boucle for).
Une autre tactique est de chercher un chiffre qui ne peut être que dans une seule case d'une certaine ligne, colonne ou carré. Si dans une colonne, il y a trois cases libres, l'une avec pour possibilités 1, 3 ou 7 et les deux autres avec 1 ou 3, il est clair que le 7 doit être dans la première. On passe donc en revue toutes les lignes, toutes les colonnes et tous les carrés, et pour chacun on prend chaque chiffre de 1 à 9 (oui ça fait encore des doubles boucles for) et on compte le nombre de cases qui peuvent le contenir : s'il n'y en a qu'une seule alors on sait où le mettre.
Avec les tactiques ci-dessus, on va éliminer beaucoup de possibilités pour chaque case et on va même découvrir la valeur de certaines d'entre elles. On va réappliquer les tactiques avec ces nouvelles informations pour faire de nouvelles déductions. Ça suffit pour résoudre les grilles faciles et intermédiaires mais pas forcément pour les plus difficiles (les grilles « expert » ou « diaboliques »).
Après avoir bien débroussaillé le problème par déduction, on peut utiliser la force brute pour finir. On a donc une méthode hybride : d'abord on réduit fortement le nombre de possibilités par déduction et ensuite (si nécessaire) on teste une par une toutes les combinaisons restantes.
La force brute a pour inconvénients de tenter beaucoup de combinaisons absurdes et d'être lente. La phase initiale de déduction élimine les combinaisons manifestement impossibles et permet à la méthode de force brute de ne tenter que des combinaisons plausibles et assez peu nombreuses — et donc d'être très efficace.
Un joueur ne tenterait la force brute qu'en (tout) dernier recours, parce que les humains ne sont pas efficaces pour faire des calculs. Il essaierait d'abord de trouver d'autres tactiques subtiles.
Même sur un ordinateur, certaines vaudraient sans doute la peine d'être implémentées. Mais d'autres n'utiliseraient pas de manière efficace le point fort des ordinateurs : faire des calculs. Il faut exploiter les outils à notre disposition selon leurs atouts. Et la meilleure stratégie pour une résolution automatisée n'est donc pas forcément la meilleure stratégie pour une résolution à la main.
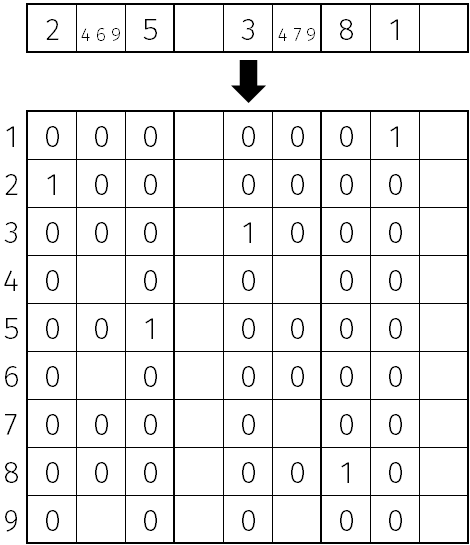
Au lieu d'un carré de neuf cases par neuf cases contenant les chiffres de 1 à 9, on peut interpréter une grille de sudoku comme un cube contenant uniquement les valeurs 0 et 1. Sur chacune des 81 cases de la grille carrée il y a une tour de neuf étages, chacun représentant un chiffre de 1 à 9.
Chacune des 9 × 9 × 9 cases indique si un certain chiffre est (on l'appelle 1) ou n'est pas (0) dans une certaine case de la grille carrée. Par exemple, « la case (1, 3, 8) vaut 1 » signifie « la case de la première ligne et troisième colonne contient un 8 ». La figure ci-contre montre comment une ligne peut devenir un carré.
La grille carrée et le cube sont parfaitement équivalents si on traduit les règles comme suit.
Il existe des techniques bien établies (programmation linéaire) permettant de résoudre ce genre de problème.
Il est assez classique pour résoudre un problème de le réinterpréter ou bien de le transformer en un autre problème qui est plus facile à résoudre. Dans le cas présent ça permet d'utiliser des techniques bien établies plutôt que de réinventer la roue. (Une fois qu'on a entré à la main les contraintes ci-dessus, on peut déléguer la résolution à des bibliothèques d'algorithmes au lieu de créer le programme soi-même.)
Une conséquence est que la résolution n'utilisera aucune des tactiques utilisées habituellement par les joueurs (c'était déjà le cas de la méthode brute, mais ici on ne cherche pas toutes les combinaisons possibles jusqu'à tomber sur la bonne). Si on utilise de l'optimisation linéaire, la résolution se fera d'autre part d'un coup (sans étapes intermédiaires). Un inconvénient est donc qu'on ne peut utiliser un tel modèle que pour trouver la solution, pas comme une aide pour apprendre des tactiques ni pour décoincer des grilles difficiles, « expert » ou « diaboliques ».
Quand on commence une grille de sudoku, on suppose qu'il existe une et une seule solution. C'est généralement une bonne hypothèse. Mais que se passe-t-il si ce n'est pas le cas ?
Si la première ligne contient 1, 2 et 3, la première colonne 4, 5, et 6, et le carré en haut à gauche a 7, 8 et 9 alors la case en haut à gauche ne peut contenir aucun des neuf chiffres et la grille n'a pas de solution.
Ça n'est pas un problème pour la méthode par force : elle teste toutes les combinaisons possibles et si elle n'en trouve pas, ça prouve qu'il n'y a pas de solution.
S'il n'y a pas de solution, les méthodes de déduction arriveront sans doute à une incompatibilité : telle case ne peut contenir aucun de neuf chiffres. Mais ça n'est pas certain : il peut être dur d'établir si une grille avec peu de chiffres donnés au départ est difficile ou impossible. (Avec une méthode hybride on a l'avantage de l'exhaustivité de la force brute pour prouver qu'il n'y a pas de solution.)
D'un autre côté, les chiffres donnés au départ peuvent autoriser plusieurs grilles valides (le extrême étant une grille entièrement vierge).
Les méthodes de pure déduction s'appuient sur des certitudes : cette case doit contenir un 2, cette autre ne peut pas contenir les chiffres 3, 6 et 7, etc. S'il y a plusieurs solutions, ces méthodes trouveront au mieux ce que ces solutions ont en commun mais ne pourront choisir entre elles (un peu comme l'âne de Buridan).
La force brute ne va sans doute trouver qu'une seule solution, même s'il y en a plusieurs (parce qu'elle est programmée pour s'arrêter dès qu'elle trouve une solution). Mais cette méthode peut très facilement être modifiée pour tester toutes les combinaisons exhaustivement, sans s'arrêter à la première solution. En revanche, ça signifierait passer beaucoup de temps sur chaque grille au cas (très improbable) où il existerait plusieurs solutions.
La méthode hybride testant toutes les possibilités après avoir éliminé autant de combinaisons invalides que possible se comportera comme la force brute. Mais, comme elle part d'un ensemble de départ nettement plus restreint, chercher toutes les solutions lui prendra nettement moins de temps.
Quand on crée un modèle mathématique, on fait des hypothèses : on ne tient pas compte de ce qui ne peut pas arriver ou qui a peu de probabilité d'arriver. S'il existe une faible chance que la solution de la grille de sudoku ne soit pas unique, est-ce que ça vaut la peine d'avoir une méthode qui peut trouver toutes les solutions ou bien va-t-on s'arrêter à la première ? En général la probabilité est quasi nulle, donc on ne va sans doute pas tenir compte de cette possibilité. Surtout si le temps de calcul pourrait être fortement augmenté ou si la méthode choisie ne marche que si on est sûr qu'il existe une solution unique.
Mais dans un contexte différent, on pourrait prendre une décision inverse. Un créateur de sudoku par exemple peut vouloir vérifier que ses grilles ont toutes une solution unique. Dans ce cas il est crucial de chercher des solutions multiples.
Il est naïf d'essayer de tenir compte de tout. Quand on conçoit un modèle, il faut sciemment ignorer certaines possibilités : ne pas tenir compte de ce qui ne fait guère de différence ou qui n'a que peu de chances d'arriver. Si on ne cherche pas un tel compromis, le résultat sera impossible à résoudre ou prendra beaucoup plus de temps que nécessaire.